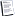
لحد العام للمتتابعة الحسابية
ح ن = أ + ( ن – 1 ) × ء
* أ هو أول حد نبداء به المتتابعة (إذا لم يشترط بداية أحرى )
* ء هو أساس المتتابعة
* ن هى رتبة الحد
* ح ن قيمة الحد
مثال (3)
فى المتتابعة ( 3 ، 7 ، 11 ، 000000 ، 487 )
• أوجد الحد السابع ؟
• أوجد رتبة الحد الذى قيمته 67 ؟
• أوجد عدد حدود المتتابعة ؟
الحل
* ح ن = أ + ( ن – 1 ) × ء
ح7 =3 + ( 7 – 1 ) × 4= 27
++++++++++++*
ح ن = أ + ( ن – 1 ) × ء
67= 3 + ( ن – 1 ) × 4
67 = 3 + 4ن – 4
67 = 4ن – 1
68 = 4ن ن = 17 #
++++++++++++*
ح ن = أ + ( ن – 1 ) × ء
487= 3 + ( ن – 1 ) × 4
487 = 3 + 4ن – 4
487 = 4ن – 1
487 = 4ن ن = 122 #
ملاحظة : -
• عدد حدود المتتابعة يساوى رتبة الحد الأخير
• ن Э ص+ دائما ً
• الأساس من النهاية هو المعكوس الجمعى للأساس من البداية
• أخر حد من البداية هو أول حد من النهاية
مثال ( 4)
اوجد الحد السابع من النهاية فى المتتابعة ( 3 ، 7 ، 11 ، 0000000 ، 487 )
الحل
• الأساس من النهاية هو المعكوس الجمعى للأساس من البداية
• أخر حد من البداية هو أول حد من النهاية
* ح ن = أ + ( ن – 1 ) × ء
ح7 =487 + ( 7 – 1)× -4 = 511
الحد السابع من النهاية = 511
مثال (5)
أي من القيمتين 151 أ، 173 ينتمى للمتتابعة الحسابية ( 13 ، 17 ، 21 ، 0000 )
الحل
ح ن = أ + ( ن – 1 ) × ء
151 = 13 + ( ن – 1 ) × 4
151 = 13 + 4 ن – 4
151 = 4ن + 9
4ن = 151 – 9 = 142
4 ن = 142
ن = 35.5 Э ص +
151 Э للمتتابعة الحسابية ( 13 ، 17 ، 21 ، 0000 )
ح ن = أ + ( ن – 1 ) × ء
173 = 13 + ( ن – 1 ) × 4
173 = 13 + 4 ن – 4
173 = 4ن + 9
4ن = 173 – 9 = 164
4ن = 164
ن = 41 Э ص +
173 Э للمتتابعة الحسابية ( 13 ، 17 ، 21 ، 0000 )
|